07 Apr 2019
|
신경망
딥러닝의 목표는 인간과 같은 활동을 하는 것을 만드는 것이다. 그래서 나온 방법이 인간의 뇌를 프로그래밍 해보자는 것. 인간의 뇌는 아래 그림과 같이 생겼다.
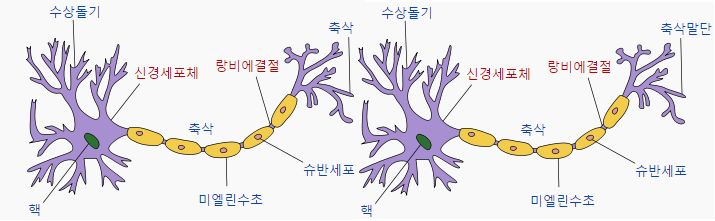
뉴런들은 이와 같이 연결 되어있는데 수상 돌기(input)에서 신호를 받아들이고 축색 돌기(output)에서 신호를 전송을 한다. 그 사이는 시냅스로 연결되어있는데 신호가 전달되기 위해서는 일정 기준(임계값 : threshold) 이상의 전기 신호가 존재해야 한다.
즉, 이 신호들의 전달을 통해서 정보를 전송하고 저장한다는 것! 이를 시스템 모델링을 하면
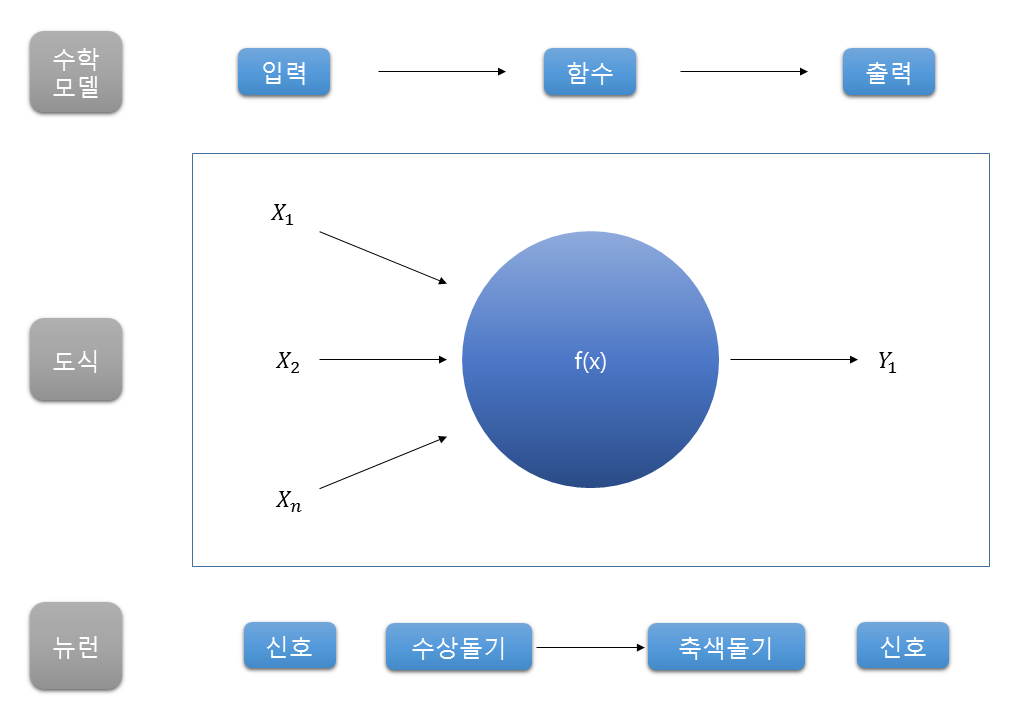
이렇게 되는데 인간은 이러한 뉴런들이 1천억개 이상, 연결은 100조개 이상이 되어있다고 한다.
1천억개의 뉴런을 간소화한 인공 신경망 구조는 아래와 같다.
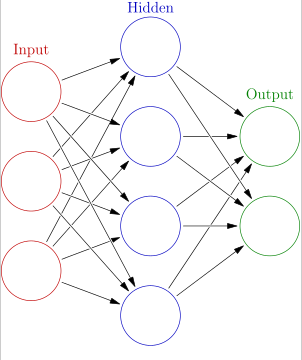
이 모델의 학습은 각 노드를 연결하는 가중치를 알아내는 것이다. 뉴런을 연결하는 시냅스의 threshold를 찾는 것처럼.
여기서 Input을 입력층, Hidden을 은닉층, Output을 출력층으로 표현을 한다. 신경망은 알아서 가중치 값을 설정하고 input, output의 예상 값을 실제 값과 비교하면서 조정해 나가면서 학습해 나간다. 이 오차를 활성화 함수와 손실함수, 경사하강법 등을 이용해 계속 줄여나가는 것이 학습이다.
신경망에는 층이 있는데 input을 제외한 hidden layer와 output layer의 층의 갯수를 통해 n층 신경망이라고 부른다. 학습이 가장 잘되는 layer와 node 갯수는 아직 발견되지 못했다. 위의 그림은 2층 신경망이다. 그러면 2층 신경망과 3층 신경망의 구현에 대해 알아보겠다.
2층 신경망 구현
from scratch.common.functions import *
from scratch.common.gradient import numerical_gradient
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis = 1)
t = np.argmax(t, axis = 1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
3층 신경망 구현
import numpy as np
def sigmoid(x):
return 1/ (1+np.exp(-x))
def relu(x):
return np.maximum(0.5,x)
def init_network():
network = {}
network['w1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
network['b1'] = np.array([0.1,0.2,0.3])
network['w2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
network['b2'] = np.array([0.1,0.2])
network['w3'] = np.array([[0.1,0.3],[0.2,0.4]])
network['b3'] = np.array([0.1,0.2])
return network
def forward(network, x):
W1, W2, W3 = network['w1'], network['w2'], network['w3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x,W1)+b1
z1 = sigmoid(a1)
a2 = np.dot(z1,W2)+b2
z2 = sigmoid(a2)
a3 = np.dot(z2,W3)+b3
y = relu(a3)
return y
network = init_network()
x = np.array([1.0,0.5])
y = forward(network,x)
이미지 출처
07 Apr 2019
|
손실함수, 경사하강법
학습
훈련데이터로부터 가중치의 최적값을 찾는 행위.
학습 시 데이터는 훈련데이터와 시험 데이터(보지 못한 new data) 2가지의 데이터가 필요하다.
하나의 data set에만 지나치게 최적화(오버피팅)되는 문제는 조심해야 한다.
손실 함수
신경망이 학습할 수 있도록 해주는 지표. 출력값과 사용자가 원하는 출력값의 차이, 즉 오차를 말한다. 이 오차를 지표로 삼아 미분을 통해 매개변수(가중치, 편향)의 기울기를 개산하고, 그 값을 줄이는 방향으로 나아간다.
평균 제곱 오차(Mean Squared Error : MSE)
계산이 간편하여 가장 많이 사용되는 손실 함수이다. 위의 식에서는 1/2를 곱하는 것으로 되어 있으나 실제로는 2가 아닌 전체 데이터의 수를 나누어 1/n을 곱해주어야 한다.
거리 차이를 제곱하는 이유: 거리 차이가 작은 데이터와 큰 데이터 오차의 차이가 커진다. 어느 부분에서 오차가 크게 나는지 쉽게 확인할 수 있다.
교차 엔트로피 오차(Cross Entropy Error: CEE)
교차 엔트로피 오차는 기본적으로 분류(Classification) 문제에서 정답(1)은 하나뿐이고 나머지는 다 오답(0)인 원-핫 인코딩(one-hot encoding)했을 경우에만 사용할 수 있는 오차 계산법이다. 교차 엔트로피 오차는 정답일 때의 모델 값에 자연로그를 계산하는 식이 된다. 아래는 -log(y)의 그래프이다.

미니배치 학습(mini-batch training)
모든 data의 손실함수를 일일이 구하고 합하면 시간이 너무 많이 소요가 되기에 랜덤하게 어느정도 data를 표본으로 뽑아서 그 표본을 대상으로 손실함수를 구하는 방법이다.
경사법(Gradient Method)
손실함수의 값을 어떻게 해야 낮출 수 있을까? 이는 기울기를 통해 할 수 있다. 손실함수에서 기울기를 편미분한 값으로 구하면 얼마나 멀리 떨어져 있는지와 어느 방향으로 가야할 지를 구할 수 있다.
먼저 data의 값을 y = w0x + w1의 직선의 함수로 값을 예측한다. 그리고 이 직선을 data와의 값을 비교해서 오차를 구한다. 이를 비용함수라고 하는데 이 비용함수를 w0을 기준으로 정사영을 한 다음 그 함수를 기준으로 학습을 한다. 미분의 값이 0에 가까워 지도록 갱신을 하는 방식이다. 이를 w1에도 적용해서 비용함수의 값을 줄이는 방향으로 w0와 w1을 조정해 나간다.
위의 수식에서 n과 비슷하게 생긴 기호는 에타인데, 이는 학습률을 나타낸다. 학습률은 값을 얼마나 갱신할지를 결정한다. 학습률이 너무 크면 발산해버려서, 너무 작으면 거의 갱신이 안되서 제대로 학습을 하지 못하기 때문에 학습률의 적절한 조정이 필요하다.
하지만 경사하강법의 단점도 있다. 미분의 값이 0일 때 그 값이 최솟값일 수도 있지만 극솟값이나 안장점(어느 방향에서는 극대, 어느 방향에서는 극소의 값을 가짐)일 수도 있기 때문이다. 이러면 학습이 제대로 안되고 멈춰버릴 가능성이 있다.
손실함수와 경사하강법의 코드
손실함수
import numpy as np
def mean_square_error(y, t):
return 0.5 * np.sum((y-t)**2)
사용 결과
>> t = [0,0,1,0,0,0,0,0,0,0]
>> y = [0.1,0.05,0.6,0.0,0.05,0.1,0.0,0.1,0.0,0.0]
>> mean_square_error(np.array(y),np.array(t))
0.097500000000000031
import numpy as np
#평균 제곱오차
def mean_square_error(y, t):
return 0.5 * np.sum((y-t)**2)
#교차 엔트로피 오차
def cross_entropy_error(y,t):
delta = 1e-7
return -np.sum(t*np.log(y+delta))
#출력 결과
>>t = [0,0,1,0,0,0,0,0,0,0]
>>y = [0.1,0.05,0.6,0.0,0.05,0.1,0.0,0.1,0.0,0.0]
>>cross_entropy_error(np.array(y),np.array(t))
0.51082545709933802
>> y = [0.1,0.05,0.0,0.0,0.05,0.7,0.0,0.1,0.0,0.0]
>> cross_entropy_error(np.array(y),np.array(t))
16.11809565095832
경사하강법
def numerical_gradient(f,x):
h = 1e-4
grad = np.zeros_like(x) #x와 같은 형상의 배열을 생성
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x)
x[idx] = tmp_val-h
fxh2 = f(x)
grad[idx] = (fxh1-fxh2) / (2*h)
x[idx] = tmp_val #값 복원
return grad
#2차원 벡터를 입력으로 받는 변수 2개의 다항함수
def function_2(x):
return x[0]**2 + x[1]**2
#출력 결과
>> numerical_gradient(function_2, np.array([3.0,4.0]))
array([ 6., 8.])
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f,x)
x -= lr*grad
return x
#출력 결과
>> init_x=np.array([3.0,4.0])
>> gradient_descent(function_2,init_x, lr=0.1, step_num=100)
array([ 6.19392843e-21, 5.60497583e-21])
#실제 최솟값인 0,0과 비슷한 결과
이미지 출처
김콜리님의 블로그
07 Apr 2019
|
활성화 함수
활성화 함수란 신호의 총합을 출력 신호로 변환하는 함수다.
(출처:http://cs231n.github.io/neural-networks-1/)

하나의 노드내에서 input data가 활성화함수에 의해 output data로 바뀌게 된다.
계단함수(step function)
그래프 모양이 임계점(threshold)을 기준으로 0 또는 1의 값을 가지게 되는 함수.
주로 퍼셉트론에서 사용한다.


Step function의 구현
import numpy as np
import matplotlib.pylab as plt
#계단함수
def step_function(x):
y = x>0
return y.astype(np.int)
x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()
시그모이드 함수(sigmoid function)
step function처럼 입력이 작으면 0, 크면 1인 것과 비선형 함수인 것은 같지만 더 매끄러운 그래프를 가짐.
매끄러운 그래프가 신경망 학습의 key point다.
비선형 함수란 y = ax + b 의 꼴로 나오는 직선의 방정식 하나로 함수의 값을 정의할 수 없는 함수다. 선형함수로 활성화 함수를 하게 되면 은닉층의 의미가 없어진다.


Sigmoid Function의 구현
import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
return 1/(1+np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()
렐루함수(ReLU function)
sigmoid function의 Gradient Vanishing 문제를 해결하기 위해 최근에 많이 사용되는 함수.
Gradient Vanishing 문제란 0과 1사이의 값을 가지는 sigmoid function에서 아주 작은 값을 가질 경우 0에 매우 가까운 값을 가지게 되는 문제. 신경망에서 많은 은닉층을 거쳐가면서 0과 가까운 값을 가지게 되면 활성화 함수에 의해 0으로 값이 수렴되어 버린다.


Relu function의 구현
import numpy as np
import matplotlib.pylab as plt
def relu(x):
return np.maximum(0,x)
x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()
소프트맥스 함수(softmax funtion)
위의 활성화 함수들은 은닉층에서 node들이 적용하는 함수라면 소프트맥스 함수는 출력츠에서의 node들이 적용하는 함수이다.
위의 식에서 y_k의 값은 0~1 사이의 값을 가지고, y_k의 값을 다 합치면 1이 나오게 되기 때문에 softmax 함수의 값을 확률로 표현한다.
Softmax funtion 구현
def softmax(x):
c = np.max(x) #연산 숫자가 너무 커지는 경우 오버플로가 발생할 수 있음
exp_x = np.exp(x-c) #오버플로 대책
sum_exp_x = np.sum(exp_x)
y = exp_x / sum_exp_a
return y
출처
활성화 함수 이미지
코드
07 Apr 2019
|
CH.1: The Worlds of Database System
1.The Evolution of DB System
Database: 체계화된 data의 모임. 여러 사람이 사용할 데이터의 집합.
data를 schema와 query를 통해 관리한다.
Schema: logical structure of the data. data-definition language 사용. 보통 data를 테이블로 표현.
Query: question about the data. data manipulation language 사용. 코딩느낌으로 data를 표현
2. Overview of a DB Management System

Main Memory(사각형 2개) - volatile
Secondary Memory(원통) - 보존
Single Box: system component
Solid Line: control, data flow
Dash Line: data flow만
File system : MS word 하나씩 일일이 수정해야함
DB : 한방에 수정가능
File system에서 파일이 10개열려 있는데 수정해야 하면 10개 다 일일이 해야함.
DB는 한번에 다른 파일까지 다 바꿈. DB의 key
사실 이 chapter는 RDBMS와 NoSQL의 비교만 하고 끝났다.

왼쪽이 RDBMS(schema) 오른쪽이 NoSQL(query). database를 관리하는 방법이 다르다.











